K-Medoids Clustering – Algorithm
The K-medoids clustering algorithm can be summarized as follows −
- Initialize k medoids − Select k random data points from the dataset as the initial medoids.
- Assign data points to medoids − Assign each data point to the nearest medoid.
- Update medoids − For each cluster, select the data point that minimizes the sum of distances to all the other data points in the cluster, and set it as the new medoid.
- Repeat steps 2 and 3 until convergence or a maximum number of iterations is reached.

Implementation in Python
To implement K-medoids clustering in Python, we can use the scikit-learn library. The scikit-learn library provides the KMedoids class, which can be used to perform K-medoids clustering on a dataset.
First, we need to import the required libraries −
from sklearn_extra.cluster import KMedoids
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
Next, we generate a sample dataset using the make_blobs() function from scikit-learn −
X, y = make_blobs(n_samples=500, centers=3, random_state=42)Here, we generate a dataset with 500 data points and 3 clusters.
Next, we initialize the KMedoids class and fit the data −
kmedoids = KMedoids(n_clusters=3, random_state=42)
kmedoids.fit(X)Here, we set the number of clusters to 3 and use the random_state parameter to ensure reproducibility.
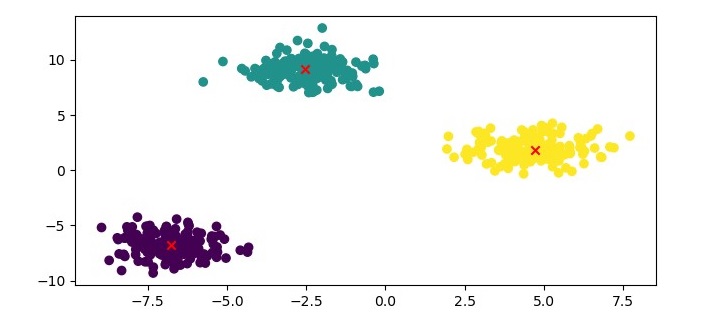
Finally, we can visualize the clustering results using a scatter plot −
plt.figure(figsize=(7.5,3.5))
plt.scatter(X[:,0], X[:,1], c=kmedoids.labels_, cmap='viridis')
plt.scatter(kmedoids.cluster_centers_[:,0],
kmedoids.cluster_centers_[:,1], marker='x', color='red')
plt.show()Example
Here is the complete implementation in Python −
from sklearn_extra.cluster import KMedoids
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# Generate sample data
X, y = make_blobs(n_samples=500, centers=3, random_state=42)# Cluster the data using KMedoids
kmedoids = KMedoids(n_clusters=3, random_state=42)
kmedoids.fit(X)# Plot the results
plt.figure(figsize=(7.5,3.5))
plt.scatter(X[:,0], X[:,1], c=kmedoids.labels_, cmap='viridis')
plt.scatter(kmedoids.cluster_centers_[:,0],
kmedoids.cluster_centers_[:,1], marker='x', color='red')
plt.show()Output
Here, we plot the data points as a scatter plot and color them based on their cluster labels. We also plot the medoids as red crosses.
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
K-Medoids Clustering – Advantages
Here are the advantages of using K-medoids clustering −
- Robust to outliers and noise − K-medoids clustering is more robust to outliers and noise than K-means clustering because it uses a representative data point, called a medoid, to represent the center of the cluster.
- Can handle non-Euclidean distance metrics − K-medoids clustering can be used with any distance metric, including non-Euclidean distance metrics, such as Manhattan distance and cosine similarity.
- Computationally efficient − K-medoids clustering has a computational complexity of O(k*n^2), which is lower than the computational complexity of K-means clustering.

K-Medoids Clustering – Disadvantages
The disadvantages of using K-medoids clustering are as follows −
- Sensitive to the choice of k − The performance of K-medoids clustering can be sensitive to the choice of k, the number of clusters.
- Not suitable for high-dimensional data − K-medoids clustering may not perform well on high-dimensional data because the medoid selection process becomes computationally expensive.
Leave a Reply